Correlation
A synonym for correlation is relationship. Therefore, the question: “Among 7th graders, what is the correlation between math and science scores?” is the same as asking, “Among 7th graders, what is the relationship between math and science scores?” Why would this be useful?
Depending on your research question, you may want to know if two things are related (or not). This relation, statistically, is referred to as a linear trend. For example, as one value (in this case, math score) improves, the other (in this case, science score) also improves. This would be a positive correlation. This and other possibilities are listed below:
| Variable 1 |
Action |
Variable 2 |
Action |
Type of Correlation |
| Math Score |
↑ |
Science Score |
↑ |
Positive; as Math Score improves,Science Score improves |
| Math Score |
↓ |
Science Score |
↓ |
Positive; as Math Score declines,Science Score declines |
| Math Score |
↑ |
Science Score |
↓ |
Negative; as Math Score improves,Science Score declines |
| Math Score |
↓ |
Science Score |
↑ |
Negative; as Math Score declines,Science Score improves |
The following graphs show the same relationships:
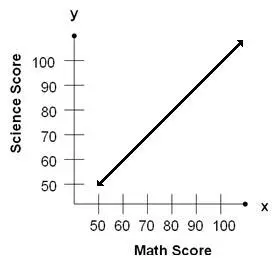
Perfect Positive Correlation

Perfect Negative Correlation
The above graphs show lines with perfect relationships. Imagine individual dots for each student along a line representing the intersection between a math and a science score. Using the perfect positive relationship example, a student scoring a 90 in math would also score a 90 in science. Repeat this in increments of 10 and you get a perfect relationship. Alternately, using the perfect negative relationship example, a student scoring a 90 in math would have a 60 in science.
However, while research tells us that there is a relationship between math and science scores, we know that it will not be perfect. The next two graphs are called scatter plots, and they show the intersection of 10 student scores (Student 1: math = 80; science = 57, for example). Notice that the perfect correlation line is still there. We chose which line to add based on the pattern we see in scores. In the first graph, the pattern seems positive, as the plotted scores suggest an upward trend. In the second, the pattern seems negative, as the plotted scores suggest a downward trend.

Positive Correlation: Math and Science

Negative Correlation: Math and Science
Finally, we can calculate a percentage that represents how close the scores are to the perfect line. The long title for this measure is called the Pearson Product Moment Correlation Coefficient. Most often, it is abbreviated as Pearson’s r, and usually noted as simply, r.* Pearson’s r is the most widely used statistical measure of association. It is measured on a -1 to 1 scale. Using a scatter plot, we plot the intersection of two measures (math and science score for a group of students) and examine the pattern. You can use Excel to create a scatter plot, called a frequency polygon, by using these directions.
*r is also one of the two most commonly reported measures of Effect Size, or strength of relationship. If asked to use effect size, you can report and interpret r. See the Effect Size review for more information.
Pearson’s r (a percentage) tells exactly how close the dots are to the line. The higher the percentage, the closer the dots (scores) are to the perfect line. A correlation of +1, for example, indicates that all scores fall exactly on a positive line. A correlation of 0 indicates no relationship, and there would be no apparent pattern to the dots. Here are some example scatter plots, with r (correlation) values.
Educational researchers are satisfied with discovering even a slight relationship. Why would .30 be acceptable? In education, we cannot control for differences between subjects in the same way that, for example, a biologist could. Many things can influence differences in test scores. A slight to moderate relationship (.35-.50), however, the findings may help focus strategies for improving both scores.
Caution: High correlation does not imply causality. You may only conclude that a linear trend exists. For example, a correlation between x (Math Score) and y (Science Score) could mean:
- x causes y (Math Score causes Science Score)
- y causes x (Science Score causes Math Score)
- A third variable affects both x & y (parent involvement affects both scores)
- Something else entirely? (students who study math also study science)
Computing and Reporting Correlations
The superintendant would like to know what relationships exist between different domains of CRCT (Criterion-Referenced Competency Test) scores. She has provided your principal with the included Excel file, “CorrelationData,” which is a random sample of 7th grade students. The students were chosen randomly in such a way that all 7th grade students had an equal chance at being selected. Since the principal knows you are taking a research course, she has asked you to complete the assignment. You use Excel to calculate correlation coefficients and to create a scatter plot. Here are some sample data. You can copy and paste into Excel. Using Excel, calculate correlation coefficients (directions below) for all pairs of scores. By looking at the table that follows, you can see which scores you need to calculate.
- Click on an empty cell that you want the correlation to be displayed in.
- Click Insert/Function (Excel 97/03) or Formulas/Insert Function (Excel 07)
- In the Search box, type Correlation. Click “Go.”
- Highlight CORREL. Click OK.
- For “Array 1,” go back to the worksheet and highlight the first set of scores you wish to correlate (click and drag).
- Alternately, if you are more familiar with formula values you can use =CORREL(A4:A93,B4:B93) for Reading and English.
Put the pointer in “Array 2,” and repeat for the second sample you wish to correlate
(click and drag). Click OK. - Excel returns the correlation coefficient between the two samples.
- Repeat as necessary for all pairs of scores.
Delete the example values in the table below and use it to display your results. This type of table is also called a correlation matrix. Notice that only half of the values are filled in. This is because data in a correlation matrix are inverse, so that Reading/English is the same as English/Reading.
Table 1. Seventh Grade CRCT Score Correlations
| Reading | English | Math | Science | Social S. | |
| Reading | 1.00 | ||||
| English | 0.87 | 1.00 | |||
| Math | 0.71 | 0.76 | 1.00 | ||
| Science | 0.74 | 0.67 | 0.71 | 1.00 | |
| Social S. | 0.80 | 0.65 | 0.98 | 0.65 | 1.00 |